Fundamental Counting Principles – why we need for Analytics!!

Hello Friends,

Welcome back !!

We have been seeing series of articles related to Probability and Statistics previously in our blog posts. Sticking the basics strongly helps to build stronger knowledge on learning complex algorithms.

• Measures of centrality facts and insights
• Measures of spreads percentiles facts and insights
• Measures of spreads range variance standard deviation

Today, we are going to our fundamentals back once again – Counting and its principles. Although this might seems very basic, but thorough knowledge on elementary counting principles ease our mathematical foundations on Machine Learning Algorithms. Refer article on Machine Learning framework –> Six modules of any machine learning applications.

Why do we need Counting?

We know for any analytics we need data. Hence we collect sample data from huge population. From the available sample data, we estimate sample statistic (mean, median, variance & standard deviation). Here we ask the question, what is the probability that the estimates we made from sample data is close to actual population? Sometimes the sample we have chosen might not be the right representative of population.

Lets take one more example of finding probability of getting 4 aces in deck of cards. In order to find this value, we need to come “Total number of possible outcomes – n” from the deck of cards (52 cards).How do you count this n? So we need counting (using counting principles) to find the value of n then we can find the probability we are interested in.

Basics of counting principle

Simple Counting:

How are numbers are there between 1 and 358 (both inclusive), super easy we can say 358. Since we had a sequence which start from 1 till 358, our answer is very straight forward. In general, “the number of numbers between 1 and n is n“. This is our fundamental counting principle – i.e. counting sequence numbers that start with 1.

Now we tweak the question and ask how many numbers are there between 73 and 358? This example is not in the form of sequence since it doesn’t start with value 1. Can we somehow make this value into a sequence? Say, we can subtract value 72 from each of the value from 73 till 358 and now we have a sequence that start from value 1 and end with 286. Now applying our fundamental principle, the number of numbers between 73 and 358 is 286.

Example of counting principle

Is there alternate way of counting that we actually dont rely on on fundamental principle that numbers should start with 1? It turns out that we have alternate method where we find the difference between 358 and 73 and add 1 to final value given as (n – k + 1).

Alternate counting principle

Going further complex, we ask this question how many numbers are there between 73 and 358 which are divisible by 7? Now we will identify numbers that are divisible by 7 and so the sequence we get is 77, 84, 92….,357. Now this sequence is a consecutive values and also not start from 1. But we already solved how to count numbers that doesn’t start from 1 earlier. We have a clue now that the new sequence will divide by value 7, apply the division and new sequence will be 11, 12, 13…., 49,50,51. Now we can resolve using n-k+1 = 51-11+1 = 41.

Counting principle with rules

Multiplication Principle

Suppose you run a food shop and offer variety of food choices. Say you offer 5 variety of South Indian dishes and 3 varieties of North Indian dishes and 3 varieties of beverages. The question we ask is how many variety of combo food choice we can offer to our customers? How do we arrive at this value?

We will start with choosing any one of South Indian dish and irrespective of any of South Indian dish we chosen, we have the choice of choosing any one of North Indian dish and again irrespective of any previous 2 dishes, we can choose any one of beverages. So the total number of choices will be 5*3*3 = 45 combos.

Multiplication rule for choice

Therefore the multiplication rule says “The number of ways of making a sequence of independent choices is just the product of the number of choice at each step“.

Multiplication Principle: Sequence with Repetition

Here we address how we can make a sequence of k objects from given n objects with repetition. Eg: You have the option to choose 10 different exercise methods like walking, dancing, playing shuttle etc… Now we can make a plan for daily by choosing any of given 10 exercise for staying fit and these exercise can be repetitive. In such case, how many weekly exercise plans can you make if you can repeat the same exercise more than one day?

This if of making a sequence of 7 items from given 10 items. For the first item in sequence we have 10 choices. Now for 2nd item in sequence again we 10 choices, since repetitive. Again by Multiplication Rule, we have 10*10*10*10*10*10*10=10^7

Multiplication rule with repetition

Hence the multiplication rule with repetition is given as “The number of sequence of k objects made from given n objects when any object in the sequence can be repeated any number of times is n^k“.

Multiplication Principle: Sequence without Repetition

How do we make a sequence where from given n objects making k objects without repetition. Similar to our previous example of choosing exercise for a week out of 10 exercise, now only difference is once the exercise chosen for day 1 cant be chosen for next day. Here the choice at each step is not independent, however number of choices at each step is independent. In this case 10*9*8*7*6*5*4=604,800.

Thus the multiplication rule for sequence without repetition is given as “The number of sequences of k objects made from given n objects such that no object in the sequence can be repeated is n(n-1)(n-2) …(n-k+1)”

Multiplication Principle: Sequence Length Equals the Number of Objects

Suppose you have 9 flower pots  and in how many ways you can arrange these 9 ports in a line. Suppose you chose 1st flower  pot and place in 1st position then we have any of balance 8 pots can be chosen for 2nd position. This is of case where n=k = 9 and the value is given as n(n-1)(n-2)…(n-k+1) which is nothing by n! (n factorial).

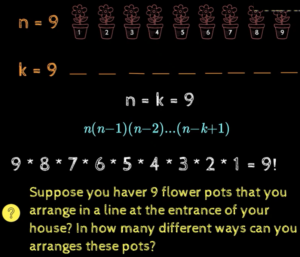
Multiplication principle: sequence length equals no of objects

Hence this is given as

• The number of sequence of length n that can be formed using n objects so that no object in the sequence is repeated is n! (0r)
• The number of ways in which n objects can be arranged amongst themselves is n! (0r)
• The number of permutations of n objects is n!

In same way no of sequences of k objects made from collection of n objects such that no object in the sequence can be repeated is n!/(n-k)!

Subtraction Principle

Till now all our counting principles examples are of rule

• “The number of choices at each step should be independent of the choices made at previous steps“
• “Address the restriction first“

What if we cant apply this? So what if the number of choices for a particular selection is dependent on the choice made by previous item?

Ex: How many 3 letter words can you form which contain at least one vowel and no letter is repeated? How do we approach this problem? Suppose we will pick 1 out of 26 alphabets for 1st letter and now we left with 25 character out of which any one letter can be selected for 2nd position of 3 letter word. This is due to condition that no letter can be repeated. Finally for filling 3rd letter we left with choice of any one vowel from 5 available vowels.

Based on our rule we know how effectively to approach this problem i.e. address the restriction first which is atleast one vowel, therefore we will start fixing the 3rd letter first with one of the vowels. Now we left with 25 characters out of which we can choose any 1 for 2nd position and similarly for 1st position we have 24 characters left and any 1 of these can be placed. But this method will ends with approach 3 letters words that always have 3rd letter with a vowel. What about words like bat, cat that does not end with vowels? No matter what position we fixing vowel, we always end with loosing some 3 letter words.

Subtraction principle example

So in this problem, we not found the solution where we end with finding all possible 3 letter words that has atleast one vowel and no letter is repeated. We are not able to apply our multiplication rule and want to approach with new solution. This issue appears is because of “At Least” in the problem.

So the way to solve the problem that has atleast is by using Subtraction Principle. This rule says “The number of objects that satisfy some condition is equal to the total number of objects in the collection minus the ones which do not satisfy this condition“.

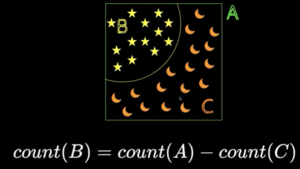
Subtraction principle formula

For our Example, A = Universal set that indicates “Set of all 3 letter words with no letter repeated”. B = “Set of all 3 letter words with no letter repeated and at least one vowel”. C = “Set of all 3 letter words with no letter repeated and no vowels”. Applied to our example. A = 26*25*24 and C = 21*20*19 and B can be found using  subtraction of C on A.

Subtraction principle example solution

With this we come to end of this article. Although basic principles of counting looks easy, applying multiplication rule varies based on the question. We need to be very strong in identifying right formula to get right values to calculate probability correctly.  We stress again fundamentals are very important and as tend to forgot these fundamentals when we move ahead in our career. We hope this article made sure to refresh your knowledge again. Share your feedback on this article and if you like this article, share with your friends. Thanks !!

Note: Inspired from https://padhai.onefourthlabs.in/  lecture series