Hello Friends,

Welcome back!!

We make humongous effort to share our knowledge on analytics world and extensively  wrote articles related to Statistics, Probability, Machine Learning. Motivation behind these articles is to understand the depth of mathematics play in making decisions and make you to unfold these basics in depth. Enjoy our some of our previous articles listed below in case if you haven’t.

 

 

Previously we also talked about importance of  Vectors and Matrices in data science space. Refer this article here –> Vectors and Matrices – What are they & Why do we care for Analytics. Especially in the world of Computer Vision and Deep Learning, Vectors and Matrix play a very major role. It is utmost import for any data scientist to have a firm grasp on Matrices. Today we will discuss on Matrix and its operation in details. Let’s begin !!

Introduction

A matrix is a rectangular array of elements enclosed in a bracket. Generally we use square bracket to represent a matrix. These numbers are called as entities or entries of a matrix. In a matrix the horizontal lines are called rows and the vertical lines are called columns. Matrix are represented by capital letters A, B, C… The elements of the matrix are represented by the lower case letters a, b, c… Matrix having only one row or one column are called as vectors.

Row vector or matrix: Any number of columns but only one row.

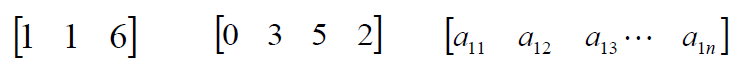
Column vector: Any number of row but only one column

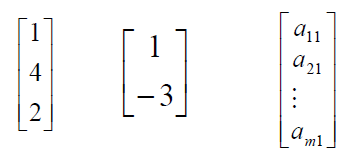
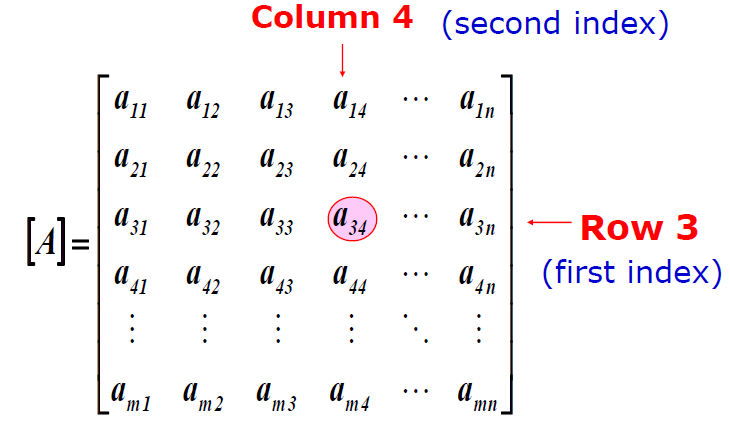
Matrix notation: Each element in the matrix is represented by the row number and the column number of the matrix.

Types of Matrix

1) Square matrix is a matrix in which the number of rows and columns are of equal.

The elements above the diagonal are called as the upper triangular elements and the elements below the diagonal are called as the lower triangular elements.

2) Diagonal matrix has only principle diagonal elements and all the other elements are 0.

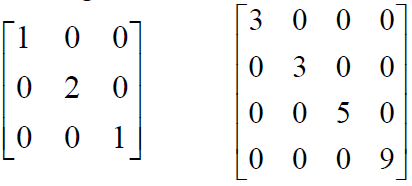
3) Unit matrix is a square matrix in which the principal diagonal elements are 1 and rest all the elements are 0. There are lot of application for unit matrix in system of equations and linear programming programs.

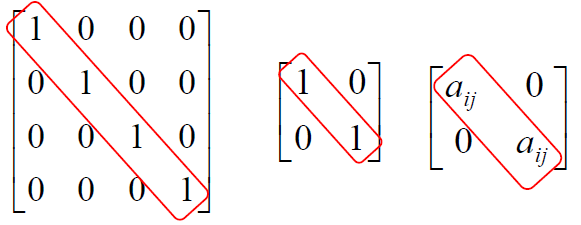
4) Null matrix is a matrix in which all the elements are 0.

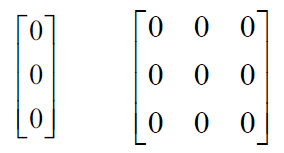
5) Upper triangular matrix is one for which the elements below the main diagonal are 0.

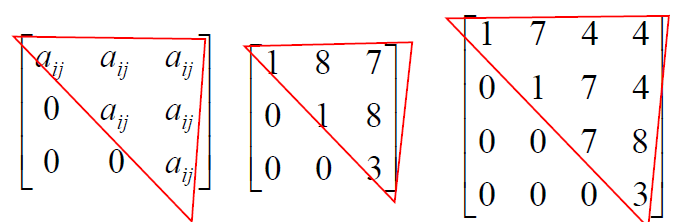
6) Lower triangular matrix is one for which the elements above the main diagonal are 0.

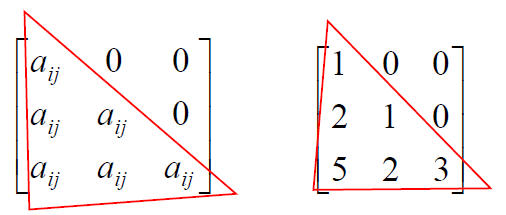
Equality of matrix

Two matrices are said to be equal when all the elements of the matrix are equal. Therefore the size and the dimensions of the matrix are also equal.

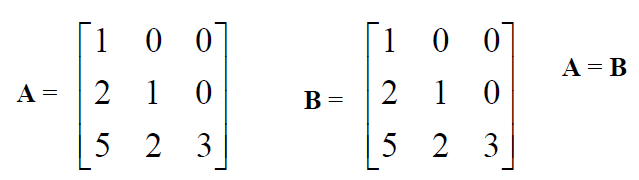
If A = B, then all Aij = Bij

Properties of equalities:

  • If A = B, then B = A for all A and B (Commutative property)
  • If A = B and B = C, then A must be equal to C (Transitive property)

Addition (and subtraction) of matrices

Only matrices of same size (order) can be added or subtracted. If A is a matrix of order 3×2, then B also should be of the order 3×2, only then either addition or subtraction of the matrices can be performed. Matrices of different sizes cannot be added or subtracted. 

Commutative law: A + B = B + A

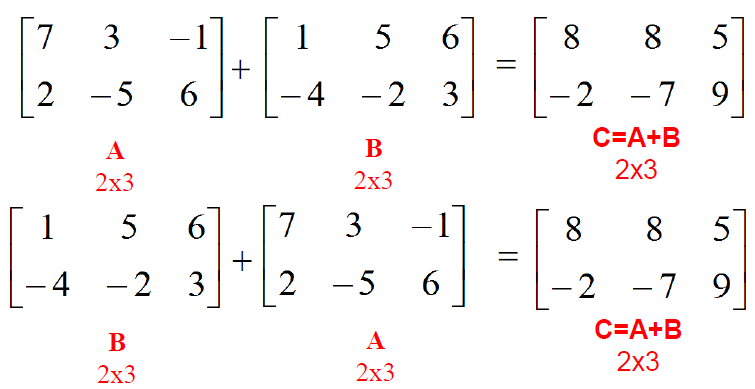
Associative property: (A + B) + C = A + (B + C)

Existence additive inverse: A + (-A) = 0

Scalar multiplication of matrices: With matrix A multiply scalar element by k (that is a constant or a single element). All the elements of the matrix should be multiplied with the scalar quantity.

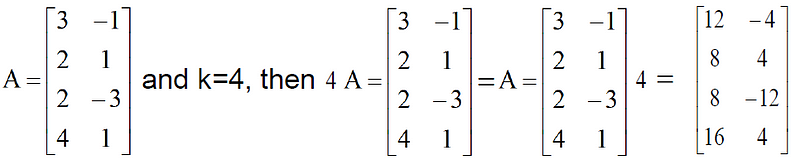
Properties:

  1. k (A+B) = kA + kB
  2. (k + g) A = kA + gA
  3. k(AB) = (kA) B = A(k)B
  4. k(gA) = (kg) A

Multiplication of matrices

The product of two matrices is another matrix. Two matrix should be conformable for the multiplication to be possible. That is Number of rows in the second matrix should be same as the number of columns in the first matrix. Matrix multiplication can be performed only if the inner dimensions of the two matrices that are multiplied are equal.

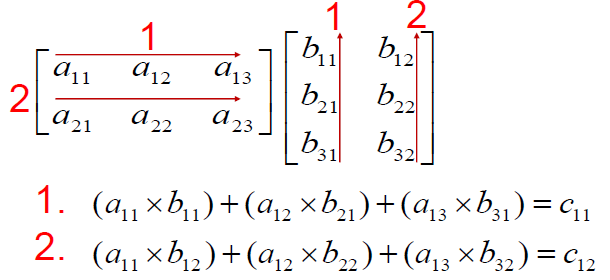
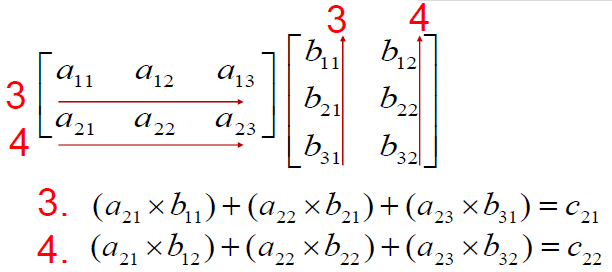
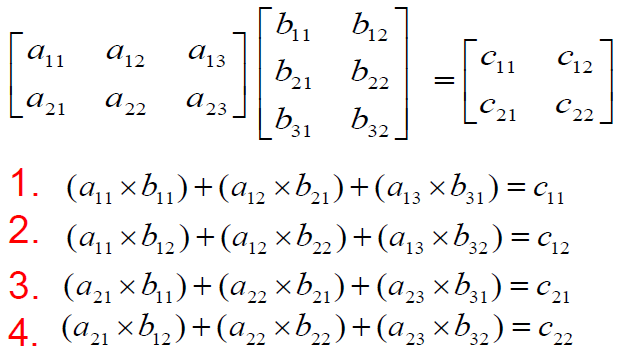
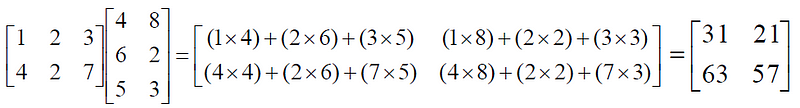
Also remember: IA = A

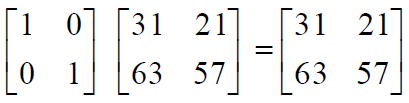
Note: AB will generally not be equal to BA. BA might not even be conformable.

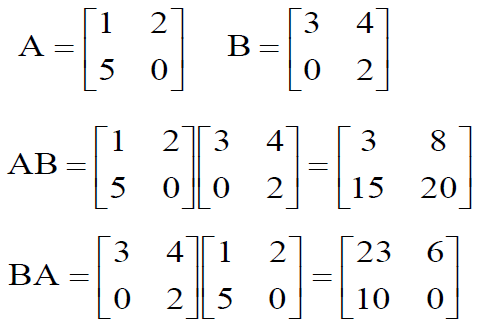
If AB = 0, neither A nor B might be a null matrix

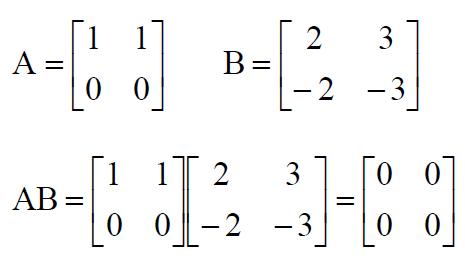
Transpose of a matrix

Interchanging the rows and the columns of a matrix is called transposing a matrix. One advantage of transpose is, if you want to multiply a rectangular matrix of order mxn (where m is not equal to n) with itself, then only way to do it is by transposing the matrix. The dimensions of A transpose is reverse of dimensions of A.

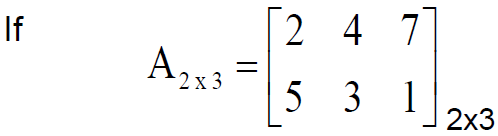
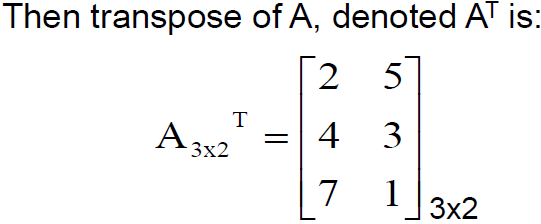
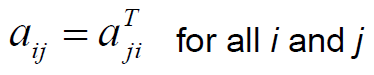
A square matrix is said to be symmetric if it is equal to the transpose of itself.

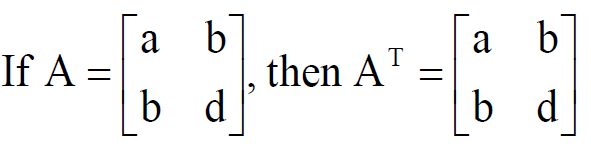
Note that transposing the matrix does not change the order of its diagonal elements. Hence, an Identity matrix, a Scalar matrix and a Diagonal matrix are always symmetric.

Inverse of a matrix

Inverse of a scalar element k is one divided by the element. Inverse of 2 is 1/2. Division of matrix is not defined. Hence inverse of a matrix is also a unique matrix which satisfies the condition that when multiplied with the original matrix, it should result in identity matrix.

Determinant of a matrix:

To compute the inverse of a matrix, the determinant of the matrix is required. Each square matrix has a unique determinant, which is a scalar value, denoted by |A|.

Minors of a matrix:

If A is a n x n matrix, then there are n x n minors obtained by determinant of a sub-matrix, deleting the row and the column of the particular element, which results in (n-1) x (n-1) matrix. It is represented by mᵢⱼ where i and j are the deleted row and column respectively.

mᵢⱼ is minor of the element aᵢⱼ in matrix A.

Example: Consider a matrix A. For the minor m₁₁ we have to delete the first row and the first column.

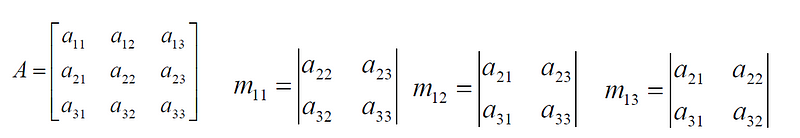
Cofactor:

Cofactor Cᵢⱼ of the element aᵢⱼ is defined as: Cᵢⱼ = (-1)ᶦ+ʲ mᵢⱼ.

Note from high school maths you might remember that the alternate elements in the calculation of determinant has negative signs. that is attributed in the multiplication of -1 with the element in odd places of the matrix. So, the determinant of the matrix A can now be summarized as:

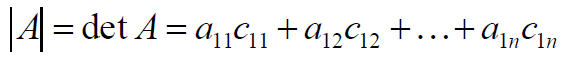
Adjoin of a matrix:

If the cofactor matrix C of a matrix A is the transpose of the cofactor matrix. It is denoted by adj(a)

adj(A) = CT

It can be shown that A (adj(A)) = (adj(A)) A = \A\ I

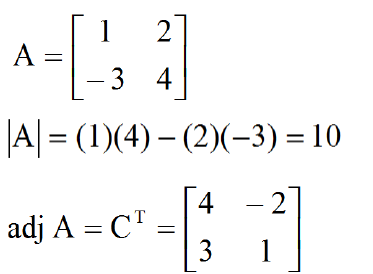
Using adjoint in matrix inversion:

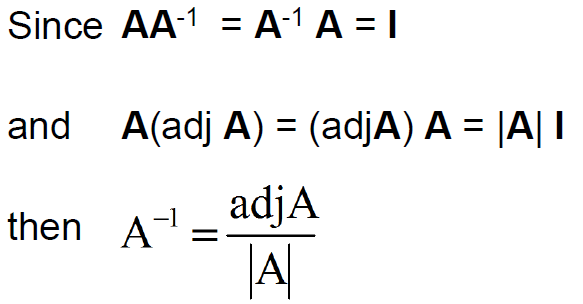
Great !! You did it. We hope you gotten the important concepts of Matrix. Application of Matrices is never ending. One cannot skip any part of data operations without getting into Matrices. This articles has just touched the surface of Matrix. This helps to build strong foundation and helps to deep dive more in this topics. Do write back your comment on improving this article and share with your friends if liked it. Will be back with one more interesting article. Till then keep learning.

<a target=”_blank” href=”https://www.amazon.in/gp/product/9332542864/ref=as_li_tl?ie=UTF8&camp=3638&creative=24630&creativeASIN=9332542864&linkCode=as2&tag=ainxt0c-21&linkId=de5c043df146b546bbd7967203e42e34″><img border=”0″ src=”//ws-in.amazon-adsystem.com/widgets/q?_encoding=UTF8&MarketPlace=IN&ASIN=9332542864&ServiceVersion=20070822&ID=AsinImage&WS=1&Format=_SL250_&tag=ainxt0c-21″ ></a>  <a target=”_blank” href=”https://www.amazon.in/gp/product/B08SML7BLY/ref=as_li_tl?ie=UTF8&camp=3638&creative=24630&creativeASIN=B08SML7BLY&linkCode=as2&tag=ainxt0c-21&linkId=a048b054e6eb00edc9f21455b30320c7″><img border=”0″ src=”//ws-in.amazon-adsystem.com/widgets/q?_encoding=UTF8&MarketPlace=IN&ASIN=B08SML7BLY&ServiceVersion=20070822&ID=AsinImage&WS=1&Format=_SL250_&tag=ainxt0c-21″ ></a>  <a target=”_blank” href=”https://www.amazon.in/gp/product/B08WX7Q7DQ/ref=as_li_tl?ie=UTF8&camp=3638&creative=24630&creativeASIN=B08WX7Q7DQ&linkCode=as2&tag=ainxt0c-21&linkId=07fad63b3ec5e37e38cbd66471e11ddc”><img border=”0″ src=”//ws-in.amazon-adsystem.com/widgets/q?_encoding=UTF8&MarketPlace=IN&ASIN=B08WX7Q7DQ&ServiceVersion=20070822&ID=AsinImage&WS=1&Format=_SL250_&tag=ainxt0c-21″ ></a>