Hello Friends,

Welcome to this tutorial on Deep Diving into Normal Distributions. This blog post is continuation of our previous blog post “Fun with functions to understand Normal Distribution“. I strongly recommend you to have a look on this post first before continuing further as you might first need to understand the mathematical functions behind Normal Distribution.

Alright !! Lets begin.

Remember the plot below ? The function Y = e^(-x^2) =  [1 /e^(x^2)]  i.e. e raise to minus x square has the shape that we are interested in – Normally Distributed. Recall When X = 0, Y = 1 i.e. Maximum value. As we keep increasing the value of X, value of Y will drop and also symmetric. Why it is Symmetric – because of “Square” in the equation. Why Y decreasing – because of “Minus” in the equation.

This kind of Shape where Peak in the Middle and dropping on either sides symmetrically is commonly found in many scenarios. Example – Scoring runs in cricket. We can see a rare chance of individual cricketer scores less than 10 runs & also scoring century. Often we can find average score has peak in middle in the range of 40-60 runs.

Having said that, I will introduce you now the formula for Normal Distributions – Probability Density Function (PDF).

Probability Density Function Formula for Normal Distribution

Note:  Q1) In above PDF equation shown, new term “1/2π”  was introduced? Where does it comes from ?

Q2) Also, notice the term . What does that 0, 1 represent ?

To find the answer, lets explore the properties of PDF.

Any Probability Density Function  pdf f(x) should satisfy 2 properties:

PDF properties

Property1: Function f(x) value should always greater than 0. We already saw in previous article that e^(-x^2) is always positive irrespective of value of X.

Property2: If we Integrate e^(-x^2) over -infinity to +infinity, we get 2π. Watch this Video for proof. To satisfy the property, value should be 1. Hence we                          bought additional 1/2π in the PDF equation. This answers our first question – Q1.

To Answer our Second Question – Q2, lets calculate Expected Value & Variance of the density function.

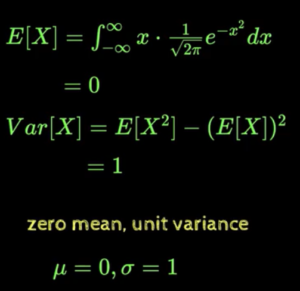
It turns out that Expected Value of PDF of Normal Distribution is “0” (recall symmetric nature, positive & negative will cancel out i.e. center of gravity is around zero). Similarly Variance is “1”.  Now   is referred as “Normal with Zero Mean and Unit Variance” density function.

Normal Distribution(Changing μ):

Here, we will vary different values of Mean keeping unit Variance constant. Formula looks as below. How did we arrive this ?

Lets substitute different values for μ. Notice the distribution gets shifted based on μ value.

Normal Distribution(Changing σ2):

Here, we keep zero mean, but try to vary different values of variance. Formula looks as below:

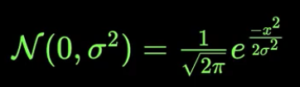
Lets substitute different values for σ. Notice the distribution gets different peakness based on σ value.

To summarize, changing μ will shift the distribution & changing σ will shrink or grow more.

Finally,

General Normal Distribution(Changing μ & σ2):

It’s the combination of above 2 formula’s. Using this we can vary different values of μ and σ  and get different combinations of Normal Distributions.

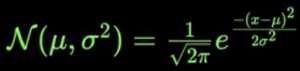
Hope,  you have gained how Normal distribution is evolved using Mathematics. Kindly leave your comments. We strongly recommend to go through below books to gain further knowledge.