Hello Friends,

Welcome Back !!

Once again i am excited to come up with another interesting topic in Deep Learning  or Machine Learning world – “Information Theory – Cross Entropy” which many of us not aware of its applications & uses.

To understand about Cross Entropy loss, we need our basic foundations which we have discussed a lot through our articles like importance of Probability, Statistics, Expected Value etc… in Analytics. Snatch our previous articles here –>

   

Random Variable – Recap

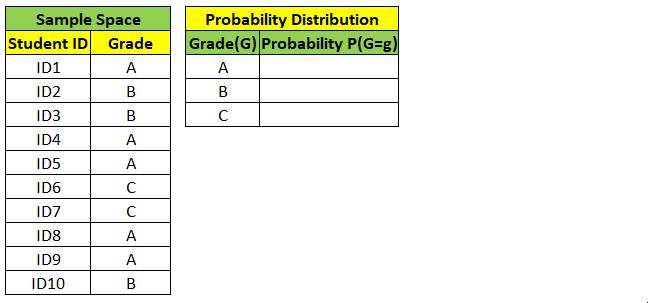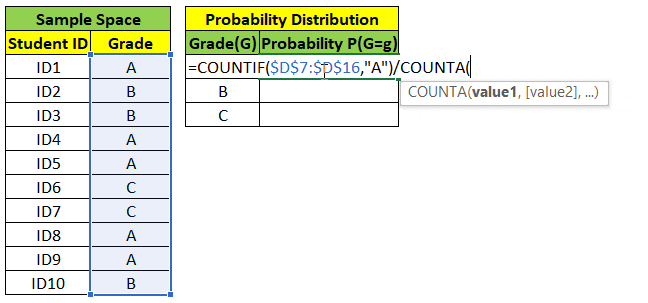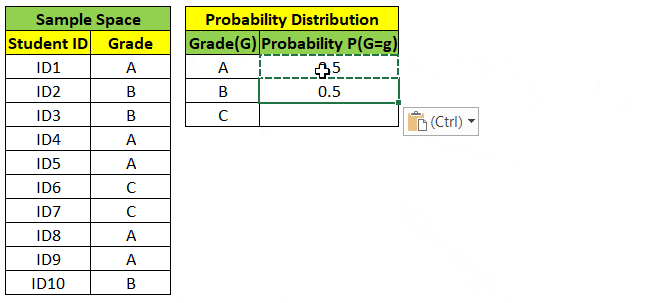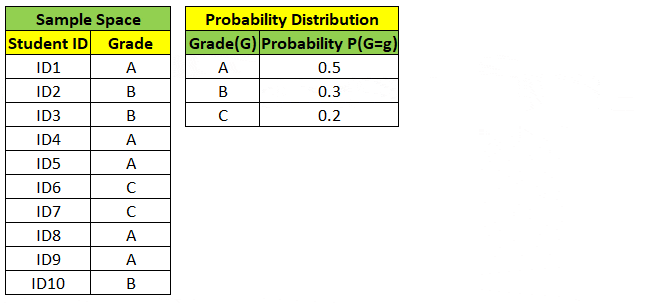
“Random Variable” is a function which maps each outcome in an event Ω to a value associated with it.

Example: As shown below, a random variable G which maps each student to one of the possible 3 values with probability associated with it.

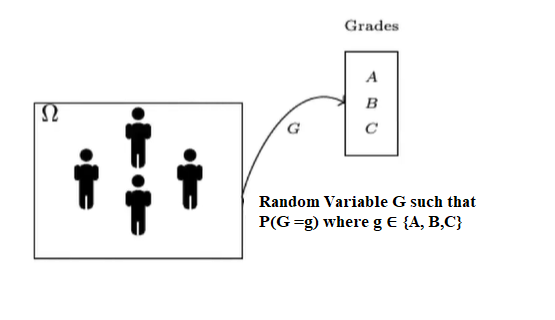
Random Variable can either take Continuous values (ex weight, height) or Discrete values (ex grade, yes/no). We can find probability distribution of Random Variable as shown below.

Cross Entropy

Introduction

Why do we recapped Random Variable ?

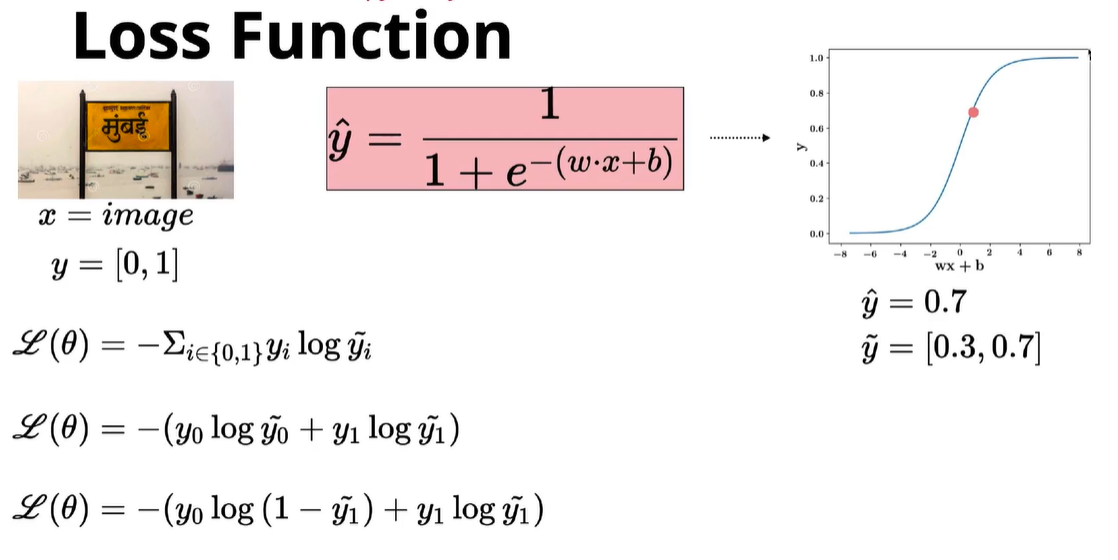
Given a classification problem to predict whether given image contains Text (Class 0)  or contains No-Text (Class 1).

ML classification model will predict the target which is Random Variable X (taking either Class 0 or 1) with probability associated of these 2 classes. Ex: ŷ = [Class 0 : 0.4, Class 1: 0.6].

We also know the True Distribution y = [Class 0: 0, Class 1: 1] i.e. we are 100% sure that given image has Text in it.

How can we compare the predicted vs actual distribution? How sure is our predicted distribution is ? Remember we might have “n” such predictions and each time we have True Vs Predicted probability distribution.

We cannot do a simple RMSE(Root Mean Square Error)  as we deal with probability values and simple RMSE will violate “Axioms of Probability”. Hence we need a different kind of loss function – enter “CROSS ENTROPY”

Expectation Value

Expected Value or Mean of a Random Variable is E(X)=μ=∑ x * P(x) i.e. random variable x multiplied by its probability. Take a look on below image for example.

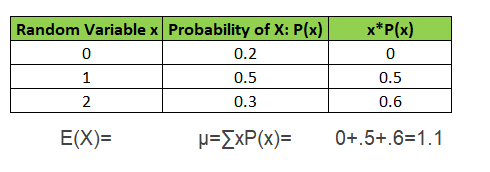
substituting values in formula,  Expected Gain E(X)=μ=∑x * P(x)=0+.5+.6=1.1E(X)=μ=∑x * P(x)=0+.5+.6=1.1

Information Content

It is a basic quantity derived from the probability of a particular event occurring from a random variable.

According to Claude Shannon’s definition,

  1. An event with probability 100% is perfectly unsurprising and yields no information.
  2. The less probable an event is, the more surprising it is and the more information it yields i.e. inversely proportional                                                                      IC(x) = log2(1/P(x)) = [log2 1 – log2(P(x))] = -log2(P(x)), since log1 =0
  3. If two independent events are measured separately, the total amount of information is the sum of the self-information’s of the individual events.

Entropy

We spoke about Random Variable which can taken different values and each values has probability thus forming distribution. Next, we looked at the information content of the event which is inversely proportional to log of probability of that event.

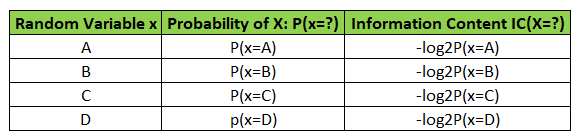
Entropy

So to find expected information content is given as E[gain]=∑P(x=i)*(-log2(P(x))) which tells average information contained in our data called as Entropy H(x).

Subscribe to our newsletters !!

Good things come to those who sign up for our newsletter
Join our email list to get the latest blog posts straight to your inbox
SUBSCRIBE
Give it a try, you can unsubscribe anytime.
close-link
Powered by balajivenky06

Cross Entropy

Now we are ready to discuss the topic that we are interested in – to compare 2 different distributions.

Given, a Random Variable x taking 4 different values,

  x ~ [A, B, C, D]

Assume,  it’s true probability associated with it represented as yi ~ P(x=A/B/C/D),

x ~ [y1, y2, y3, y4]

Hence, we can find it’s Information Content,

IC(x) ~ [-log2y1, -log2y2, -log2y3, -log2y4]

Original Entropy which gives average information content of True Distribution,

H(y) = -∑ yi * log yi  where i = 1,2,3,4

Our Machine Learning model will estimate probability ŷ,

x̄ ~ [ŷ1, ŷ2, ŷ3, ŷ4]

and its information content as,

IC(x̄) ~ [-log2ŷ1, -log2ŷ2, -log2ŷ3, -log2ŷ4]

Entropy of Estimated distribution i.e. Cross Entropy,

H(y, ŷ) = -∑ yi * logŷi  where i = 1,2,3,4

Our goal is to find the difference of Entropy & Cross Entropy, lead us to “KL Divergence” formula.

KL Divergence

Also known as  Kullback-Leibler Divergence (KL divergence), or relative entropy – gives a score that measures the divergence of one probability distribution from another.

KL Divergence = (y||ŷ) = H(y, ŷ) – H(y)

                                                                         = -∑ yi * logŷi – (-∑ yi * log yi)

                                                                           = -∑ yi * logŷi  + ∑ yi * log yi

in terms of ML, we need to minimize this loss for better prediction

KL Divergence = (y||ŷ) = min{-∑ yi * logŷi  + ∑ yi * log yi}

Consider, we use logistic regression as our classification model (can be any algorithm), which uses Sigmoid function  for prediction.

                                                         σ(x) = 1/(1+exp(-x))

          = 1 / (1 + exp(-(w*x +b)) where w & b represents slope & intercept of sigmoid function

So, our KL Divergence minimization optimization is with respect to parameters w, b

KL Divergence = (y||ŷ) = min w, b {-∑ yi * logŷi  + ∑ yi * log yi}

we know only ŷ which is predicted probability using sigmoid function is dependent on parameters w, b

KL Divergence = (y||ŷ) = min w, b {f(w,b) + C} i.e. True probability distribution is constant

                                                                                                     = min w, b {-∑ yi * logŷ} = H(y, ŷ)

So, in practice entire “KL divergence equation boils down only to minimization Cross Entropy formula“.

Cross Entropy

Example

Taking our example of predicting whether image has Text or No Text.

Given, image with Text. So True Probability is [1, 0]

Say, our ML model predicted probability as [0.7, 0.3]

Substituting in Cross Entropy Formula

H(y, ŷ) = -∑ yi * logŷi

                                                                                                                                             = – (1*log2(0.7) + 0*(log2(0.3))

                                                                                                                                      = – (1*log2(0.7)) , since second term is 0

                                                                                                                                      = -log2(0.7)

                                                                                                                                       ~ -logŷc, where c represents True class

So, we can “directly take negative log of  predicted probability for True Class” (in our case image has Text is True Class) to find loss value.

Simplified Cross Entropy

In any case, True class can be varied. A given image may have Text or No Text & it’s true class will be varied accordingly. Hence we need to modify the formula to adjust accordingly

Cross Entropy

Conclusion

We started with why RMSE cant be used as a loss function to compare 2 different probability distributions. Hence we need for different loss functions using information theory developed by Claude Shannon.

We saw about,

Expected Value E(x) = ∑x * P(x), since x is a random variable that takes different values with probability associated with it.

Information Content IC(x) = -log2(P(x)), rare an event – more the information content

Entropy H(x) = ∑P(x=i)*(-log2(P(x))), that computes average information content using Expected value formula

KL Divergence (y||ŷ)= min w, b {-∑ yi * logŷ}, measures how one probability distribution is different than other

And approximated KL Divergence equation to Cross Entropy H(y, ŷ) = -∑ yi * logŷi , average information content of predicted probability distribution

Finally, Simplified to -((1-y)log(1-ŷ) + ylogŷ), which will work whatever may be our True distribution is….

Cross Entropy loss is almost used in all Deep Learning and Machine Learning classification models when the output is in probability for different classes. Hope you like this article, if so please share with your friends and leave a comment. Till we come back with another interesting topic, keep reading !!