Hello Friends,

Welcome Back !!

Previous article we saw the founding principles of Counting. Click here for the article –> Fundamental Counting Principles – why we need for Analytics. There we discussed the basic formula for counting and addressed how to count in a sequence using Multiplication & Subtraction Principles. Also we discussed how to count the sequence with repetitions and without repetitions. Knowing these founding principles of counting helps to have command in while working with data.

 

 

Some of our other articles on Statistics Primer:

Introduction

Today’s we will continue our journey of basics and continuing previous articles on Counting Principles – we’ll discuss about Collections. We saw in Sequence order matters i.e. CAT ≠ ACT. Even though both words have the same letters but we wont consider as single word.

But in “Collections” – order does not matter i.e. CAT = CTA = ACT = ATC = TAC = TCA.

In Sequence we come up formula n! / (n-k)! to find the no of sequences without repetitions given a condition. Now instead of sequence, how many collections without repetitions can be formed with given conditions ? We don’t know yet!!

We know how to count sequences. For More info –> Fundamental Counting Principles – why we need for Analytics. Can we make use of that knowledge to count collections? Yes:)

Let’s take our example of finding No of 3 letter words from 26 alphabets.

Example of Sequence

As we saw earlier, lets breakdown the solution of this problem in 2 steps.

  • Step1: select any 3 letter to put in blank and form a word. Let’s take “CAT”.
  • Step2: Now we can arrange these 3 characters in different orders to form 3! words (like ACT, TAC etc…).

So to generalize, select k items to be put in the sequence and re-arrange the k items in k! ways.

Collections Generalization

Since in collections, order is not important, we are interested only in how many such k items – (N) can be formed from a given set of n items ?

Say, N = Number of ways of selection k elements, k! = number of ways of re-arranging the k terms, then we know the formula for No of Sequences.

                                                                                       Number of Sequences  = N * k! = n! / (n-k)!

From this we can calculate No of Collections N = n! / ((n-k)! * k!) –> “This formula for Without Repetitions”

Collections Formula

Collections Formula

Note: Intuitively this formula makes sense because in collections, we not bothered about arrangements. Hence we divide the Number of Sequence formula by another k! which represents no of re-arrangements.

Collections(With Repetitions)

With repeat, the item selection can be repeated. We will take an example as below and intuitively derive the equation. A food shop offering 10 different varieties of breakfast. How many breakfast combos containing 5 items  can you form if you are allowed to have multiple servings of the same dish?

Collections with repetition

By now we know n = 10 i.e. Total different varieties of breakfast provided. k = 5 i.e. no of items to be mixed to form a combo. Say, when we choose any one of dish (like Burger..) and start making the combo, so now we left with  k-1 = 4 items to fill the combo. Since repetition is allowed, we can again choose the same item i.e. Burger to fill the 2nd slot i.e. this combo comes with 2 burgers, now left with k-2 = 3 items still left to fill.

Can we have all 5 items in a combo being ending up with same item ? Yes, as far as repetition is allowed. So chance of same item being repeated after choosing for the 1st time is k-1 times i.e. 4 times for our case. Now the problem boils down to choose k items from n+k-1.

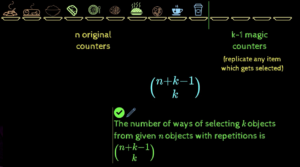
Collections with Repetition Formula

Collections with Repetition Formula

Collections + Multiplication Principle

Given a class of 7 boys and 8 girls, in how many ways can you form a committee of 4 members with 2 boys and 2 girls?

We can think of breaking the problem in to 2. First, we can find choosing 2 boys out of 7 boys and similarly 2 girls out of 8 girls and the final answer will be product of 2 outcomes. 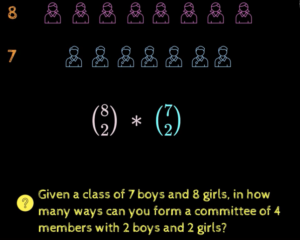Collections Multiplication

Whenever, we are given with n items  of i different types (i.e. in our example 2 different type – Boys & Girls), then m1+m2+….+mn=n. And we want to form a collection of k items (i.e. 2 items from boys & 2 items from girls), then k1+k2+….+kn = k. Then in order to solve this, we need to solve each of these cases individually.

Multiplication + Subtraction Principle

Suppose we have a hospital which contains 5 different types of specialists – 3 cardiologists, 2 – neurologists, 4 – diabetologists, 5 – gynecologists & 7 – general physicians. Totally 21 doctors. Suppose we need to find in how many ways can you form a 4 member committee containing at least one gynaecologists?

Here we cant simple says 21 choose 4, why ? 4 can be other than gynaecologists. But we need a committee which must include atleast one gynaecologists.

Collections Subtraction Principle

Atleast – is the key word which cause the problem. In such cases we will go for subtraction principle.

Say, in Set A = We have all possible committees of 4 members ; Set B = All possible committees containing at least one gynaecologists. Therefor Set C = Represents all possible committees containing no gynaecologists.  If finding Set A & Set C, we can easily get the answer for Set B.

Set A = Choosing 4 out of 21 doctors. Similarly Set C = Choosing 4 out of 16 doctors ( Why subtract 5 gynaecologists out of total 21 doctors).  Finally subtracting C from A, we can get the interested value of B.

Conclusion

With this we come to end of this article. Although basic principles of counting looks easy, applying multiplication rule varies based on the question. We need to be very strong in identifying right formula to get right values to calculate probability correctly.  We stress again fundamentals are very important and as tend to forgot these fundamentals when we move ahead in our career. We hope this article made sure to refresh your knowledge again. Share your feedback on this article and if you like this article, share with your friends. Thanks !!

<a target=”_blank” href=”https://www.amazon.in/gp/product/0735611319/ref=as_li_tl?ie=UTF8&camp=3638&creative=24630&creativeASIN=0735611319&linkCode=as2&tag=ainxt0c-21&linkId=1710a2e9c47c29a0f9fdac95205563d2″><img border=”0″ src=”//ws-in.amazon-adsystem.com/widgets/q?_encoding=UTF8&MarketPlace=IN&ASIN=0735611319&ServiceVersion=20070822&ID=AsinImage&WS=1&Format=_SL250_&tag=ainxt0c-21″ ></a> <a target=”_blank” href=”https://www.amazon.in/gp/product/067009532X/ref=as_li_tl?ie=UTF8&camp=3638&creative=24630&creativeASIN=067009532X&linkCode=as2&tag=ainxt0c-21&linkId=706d6efe9c54c4601d014cfeda744db8″><img border=”0″ src=”//ws-in.amazon-adsystem.com/widgets/q?_encoding=UTF8&MarketPlace=IN&ASIN=067009532X&ServiceVersion=20070822&ID=AsinImage&WS=1&Format=_SL250_&tag=ainxt0c-21″ ></a> <a target=”_blank” href=”https://www.amazon.in/gp/product/0670092169/ref=as_li_tl?ie=UTF8&camp=3638&creative=24630&creativeASIN=0670092169&linkCode=as2&tag=ainxt0c-21&linkId=1ee3c3fb4075f068e910b68d6634d0c9″><img border=”0″ src=”//ws-in.amazon-adsystem.com/widgets/q?_encoding=UTF8&MarketPlace=IN&ASIN=0670092169&ServiceVersion=20070822&ID=AsinImage&WS=1&Format=_SL250_&tag=ainxt0c-21″ ></a>

Note: Inspired from https://padhai.onefourthlabs.in/  lecture series