Deep Learning on Types of Activation Functions !!

Hello Friends,

Welcome Back !!

Hope you are enjoy reading our articles. Today we are back with another important and interesting articles on “Deep Learning Activations Functions“.

Deep learning is a branch of machine learning which is completely based on artificial neural networks, as neural network is going to mimic the human brain. With accelerated computational power and large data sets, deep learning algorithms are able to self-learn hidden patterns within data to make predictions.

Refer our article –> https://ainxt.co.in/temperature-prediction-with-tensorflow-dataset-using-cnn-lstm for understanding & applying Tensorflow, a deep learning framework for predictions.

Deep Learning

In this article, we will discuss one of the important concept that revolutionized “Deep Learning” World – “THE ACTIVATION FUNCTIONS”

• https://ainxt.co.in/complete-guide-to-clustering-techniques/
• https://ainxt.co.in/how-confident-are-you-with-confident-intervals/
• https://ainxt.co.in/deep-diving-into-normal-distribution-function-formula/

Introduction

Activation function decides whether a neuron should be activated or not by calculating weighted sum and further adding bias with it. The purpose of the activation function is to introduce non-linearity into the output of a neuron.

An activation function in a neural network defines how the weighted sum of the input is transformed into an output from a node or nodes in a layer of the network. Sometimes the activation function is called a “transfer function” and many activation functions are nonlinear.

Elements of a Neural Networks

Input layer: This layer accepts input features. It provides information from the outside world to the network, no computation is performed at this layer, nodes here just pass on the information to hidden layer.

Hidden Layer: Nodes of this layer are not exposed to the outer world, they are the part of the abstraction provided by any neural network. Hidden layer performs all sort of computation on the features entered through the input layer and transfer the result to the output layer.

Output Layer: This layer brings up the information learned by the network to the outer world.

Activation Function Formula

Propagation

Forward Propagation:

Forward propagation refers to the calculation and storage of intermediate variables for a neural network in order from the input layer to the output layer.

Neural networks take several inputs, processes it through multiple neurons from multiple hidden layers and returns the result using an output layer. This process is known as Forward propagation.

Backward Propagation:

Backward propagation refers to the method of calculating the gradient of neural network parameters. In short, the method traverses the network in reverse order, from the output to the input layer, according to the chain rule from calculus.

When if the estimated output is far away from the actual output (high error). We update the biases and weights based on the error. This weight and bias updating process is known as Back propagation.

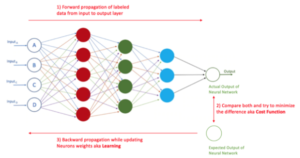
Propagation

Types of Activation Function

1) Linear Function

Linear function has the equation similar to as of a straight line i.e. y = Wx + b

It takes the input (Xi’s) multiplied by the weights (Wi’s) for each neuron and creates an output proportional to the input. In simple term, weighted sum input is proportional to output.

Problem with Linear Function:

• Differential result is constant
• All layers of the neural network collapse into one

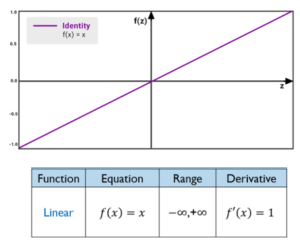
Linear Function

2) Binary Step Function

The Binary step function would be a threshold based classifier. i.e. whether or not the neuron should be activated based on the value from the linear transformation.

Pros and Cons:

• The gradient of the binary step function is zero, which is the very big problem in back prop for weight updation
• Binary step function is handling binary class problem alone

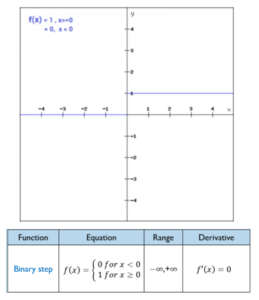
Binary Function

3) Sigmoid Function

Sigmoid function is one of the most widely used non-linear activation function. Sigmoid transforms the values between the range 0 and 1.

Pros:

• The output of the sigmoid function always ranges between 0 and 1
• Sigmoid is S-shaped, “monotonic” and “differential” function
• Derivative/Differential of the sigmoid function (f(x)) will lies between 0 and 0.25
• Derivative of the sigmoid function is not “monotonic”

  Cons:

• Derivative of sigmoid function suffers “Vanishing gradient and Exploding gradient problem”
• Sigmoid function in not “zero-centric” This makes the gradient updates go too far in different directions. 0 < output < 1, and it makes optimization harder
• Slow convergence as its computationally heavy

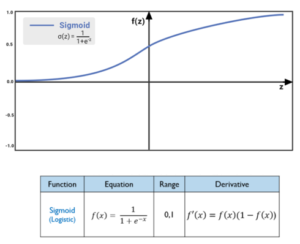
Sigmoid Function

4) Tanh Function

The tanh function is very similar to the sigmoid function. The only difference is that it is symmetric around the origin. The range of values in the case is from -1 to 1. Thus inputs to the next layer will not always be of the same sign.

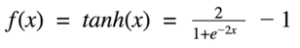
Tanh Formula

Pros:

• The function and its derivative both are monotonic
• Output is zero “centric”
• Optimization is easier
• Derivative/Differential of the Tanh function (f(x)) will lies between 0 and 1

Cons:

• Derivative of Tanh function suffers “Vanishing gradient and Exploding gradient problem”
• Slow convergence as its computationally heavy

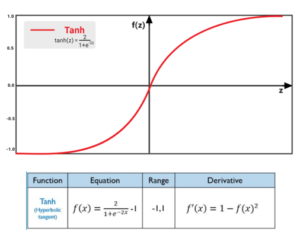
Tanh Function

5) ReLU

The ReLU function is another non-linear activation function that has gained popularity in the deep learning domain. ReLU stands for Rectified Linear Unit.  The main advantage of using the ReLU function over other activation function is that it does not activate all the neurons at the same time.

This means that the neurons will only be deactivated if the output of the linear transformation is less than 0.

Pros:

• The function and its derivative both are monotonic
• Main advantages of using the ReLU function – It does not activate all the neurons at the same time
• Computationally efficient
• Derivative/Differential of the Tanh function (f(x)) will be 1 if f(x) > 0 else 0
• Converge very fast

Cons:

• ReLU function is not “zero-centric”. This makes the gradient updates go too far in different directions. 0 < output < 1, and it makes optimization harder
• Dead neuron is the biggest problem. This is due to Non-differentiable at zero

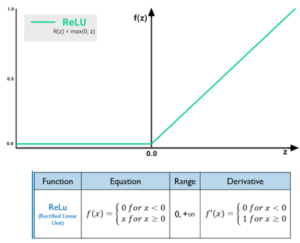
ReLU Function

6) Leaky ReLU

Leaky ReLU function is nothing but an improved version of the ReLU function, As we saw that for the ReLU function, the gradient is 0 for x<0, which would deactivate the neurons in that region.

Leaky ReLU is defined to address this problem, instead of defining the ReLU function as 0 for negative values of x, we define it as an extremely small linear component of x.

Pros:

• Leaky ReLU is defined to address problem of dying neuron/dead neuron
• Problem of dying neuron/dead neuron is addressed by introducing a small slope having the negative values scaled by a enables their corresponding neurons to “stay alive”
• The function and its derivative both are monotonic
• It allows negative value during back propagation
• It is efficient and easy for computation
• Derivative of Leaky is 1 when f(x) > 0 and ranges between 0 and 1 when f(x) < 0

Cons

Leaky ReLU does not provide consistent predictions for negative input values

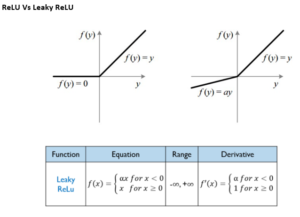
Leaky ReLU

7) Exponential Linear Unit

Exponential Linear Unit for short is also a variant of Rectified Linear Unit (ReLU) that modifies the slope of the negative part of the function. Unlike the leaky ReLU and parametric ReLU functions, instead of a straight line, ELU uses a long curve for defining the negative values.

Pros:

• ELU is also proposed to solve the problem of dying neuron
• No Dead ReLU issue
• Zero-centric

 Cons:

• Computationally intensive
• Similar to Leaky ReLU, although theoretically better than ReLU, there is currently no good evidence in practice that ELU is always better than ReLU
• F(x) is monotonic only if alpha is greater than or equal to 0
• Slow convergence due to exponential function
• F¹(x) derivative of ELU is monotonic only if alpha lies between 0 and 1
  

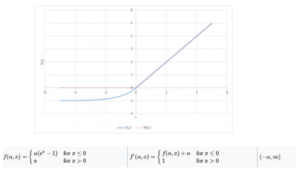
  Exponential Leaky Unit

8) Parameterized ReLU

This is another variant of ReLU that aims to solve the problem of gradient’s becoming zero for the left half of the axis. The parameterized ReLU, as the name suggests, introduces a new parameter as a slope of the negative part of the function.

Pros:

• The idea of leaky ReLU can be extended even further
• Instead of multiplying x with a constant term we can multiply it with a “hyperparameter” which seems to work better the leaky ReLU. This extension to leaky ReLU is known as Parametric ReLU
• The parameter α is generally a number between 0 and 1, and it is generally relatively small
• Have slight advantage over Leaky ReLU due to trainable parameter
• Handle the problem of dying neuron

Cons:

• Same as leaky ReLU
• F(x) is monotonic when a> or =0 and f¹(x) is monotonic when a=1

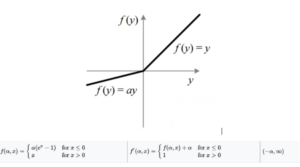
Parameterized ReLU

9) Swish

Swish is a lesser known activation function which was discovered by researchers a Google. Swish is computationally efficient as ReLU and shows better performance than ReLU on deeper models. The values for swish ranges from negative infinity to infinity.

The curve of the swish function is smooth, and the function is differentiable at all points. This is helpful during the model optimization process and is considered to be one of the reasons that swish outperforms ReLU.

Swish function is “not monotonic”. This is means that the value of the function may decrease even when the input values are increasing.

Swish Activation Function

10) Softmax

Softmax function is often described as a combination of multiple sigmoid. We know that sigmoid returns values between 0 and 1, which can be treated as probabilities of a data point belonging to a particular class. Thus sigmoid is widely used for binary classification problems.

The Softmax function can be used for multiclass classification problems. This function returns the probability for a data point belonging to each individual class.

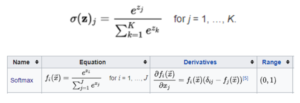
Softmax Function

Derivatives of Activation Functions

Let us see the derivatives of all the above activation functions:

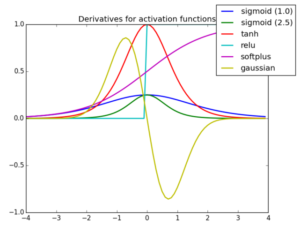
Derivatives of Activation Functions

Conclusion

Thus said, we have come to end of this long article. Activation Functions are still active research topic and there are many more functions being discovered and used in Deep Learning Techniques. Activation Functions are one of the Hyper-Parameter Tuning in Deep Learning networks which means we cannot judge which activation function will give better result in accuracy. Hence, we need to train our model with different activation functions and observe for performance. But mostly industry prefers Sigmoid and ReLU more as these have performed better than others.

Thanks for staying there and reading this article of “Activation Functions“. Hope that we have covered most of the topics related to this topic we have chosen. We hope this helps to refresh your knowledge on this topic. Let us know your feedback on this article and share us your comments for improvements. We will come with interview guide on next topic, till then enjoy reading our other articles.